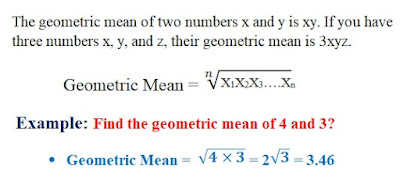what Is The Relation Between Mean Median And Mode
In statistics, there is a Relation Between Mean Median And Mode for a distribution that is somewhat skewed. The "empirical relationship" between the mean, median, and mode is defined as follows: the mode is equal to the difference between three times the median and two times the mean.
what is the Relation Between Mean Median And Mode
What is the Mean?
The most common way to measure central tendency is with the mean. In actuality, it depicts the average of the specified data set. It works with both discrete and continuous data.
It is calculated by dividing the total number of values in the data collection by the sum of all the values in the collection.
If a set of data contains n values, such as x1, x2, x3,..., xn, then the mean of the data is as follows:
It may also be represented by:
RS Aggarwal Quantitative Aptitude Fully Solved
Area Formula For Triangle Mind Blowing Tricks
Mean of Negative Numbers
Up until now, we have seen examples of how to find the mean of positive numbers. However, what happens if there are negative numbers in the observation list? Let's clarify using an example.
For instance:
Determine 9, 6, -3, 2, -7, 1's mean.
Answer:
First, add up all the numbers:
Sum: 9 + 6 + (-3)+2 + (-7)+1
= 8 + 6-3 + 2-7 +1
To find the mean, divide the total by 6.
Mean is 8./6, or 1.33.
what is the Relation Between Mean Median And Mode
Type of Mean
In statistics, mean values come in three main varieties that you will learn about.
1. Arithmetic of Mean
2. Geometric Mean
3. Harmonious Mean
1. Arithmetic of Mean
The term "arithmetic mean" refers to the total of all the values divided by the total number of values. To compute, simply multiply the total number provided by the number of numbers provided.
Example:- find the mean of 3, 5, 9, 5, 7, 2.
Add up all of the provided numbers now:
31 = 3 + 5 + 9 + 5 + 7 + 2
Divide that amount now by the total number of numbers in the sequence:
316 = 5.16
5.16 is the solution.
2. Geometric Mean
3. Harmonious Mean
Relation Between Mean Median And Mode pdf and with example |
The formula provides the Relation Between Mean Median And Mode pdf and with example that is the three measures of central tendency for a distribution that is moderately skewed.
Mode = 3 Median – 2 Mean
Another name for this
relationship is an empirical relationship. When we know the other two measures
for a given set of data, this is used to find one of the measures. The LHS and
RHS can be switched to rewrite this relationship in various ways.
Range
The range in statistics is the
variation between the sets highest and lowest data value. The equation is:
Range = Highest value – Lowest value
Relation Between Mean Median And Mode pdf and with example
Example Problem
Determine the given data's mean, median, mode, and range:
Question: 90, 70, 69, 65, 89, 85, 53, 47, 61, 27, 80, 94, 53, 68, 79, 94, 53, 65, 87,
Answer:
Given
90, 70, 69, 65, 89, 85, 53, 47, 61, 27, 80, 94, 53, 68, 79, 94, 53, 65, 87,
👉 There are twenty observations.
- Mean is = (total observations) / Number of observations.
= (90 + 70 + 69 + 65 + 89 + 85 + 53 + 47 + 61 + 27 + 80)/20 + 94 + 53 + 68 + 79 + 94 + 53 + 65 + 87
1419/20 = 70.95
= The mean is thus 70.95.
Relation Between Mean Median And Mode pdf and with example
- Median
The following are the observations in ascending order:
27; 47; 53; 53; 61; 65; 65; 68; 69; 70; 79; 80; 85; 87; 89; 90; 90; 94, 94
Thus, n = 20
= 1/2 [(n/2) + (n/2 + 1)] is the median.
The = 1/2 [10 + 11] observations
= 1/2 (69 + 70)
= 139/2 equals 69.5
The median is 69.5 as a result.
Relation Between Mean Median And Mode pdf and with example
- Mode
53 is the value that appears the most frequently in the provided data.
Consequently, mode = 53
Range is defined as Highest - Lowest value.
= 27 – 94
= 67
what is the Relationship Between Mean Median And Mode
There are three distinct formulas that we can use to find the mean for grouped data.
In statistics, there is a Relationship Between Mean Median and Mode for a distribution that is somewhat skewed. The empirical Relationship Between Mean Median and Mode is described as follows: the mode is equal to the difference between three times the median and two times the mean. Below is a detailed discussion of this relationship.
To remember,
What is the Relationship Between Mean Median and Mode
By adding together all of the data values and dividing the result by the total number of data sets, the mean, or average, of the data set is determined.